5 logische Rätsel, um Muster zu finden

Anstelle eines Fragezeichens sollte der Kreis die Nummer 253 enthalten. Dies ist das Prinzip, nach dem Zahlen in Kreisen gebildet werden: Jede vorherige Zahl wird mit 2 multipliziert und 3 zum Ergebnis addiert.

1 × 2 + 3 = 5.
5 × 2 + 3 = 13.
13 × 2 + 3 = 29.
29 × 2 + 3 = 61.
61 × 2 + 3 = 125.
125 × 2 + 3 = 253.

Oder hier ist eine andere Art der Lösung: Zu jeder vorherigen Zahl wird 2 zur n-ten Potenz addiert.

1 + 2² = 1 + 4 = 5.
5 + 2³ = 5 + 8 = 13.
13 + 2⁴ = 13 + 16 = 29.
29 + 2⁵ = 29 + 32 = 61.
61 + 2⁶ = 61 + 64 = 125.
125 + 2⁷ = 125 + 128 = 253.

Anstelle eines Fragezeichens sollte der Buchstabe "P" im Quadrat stehen. Die Summe der Zahlen in jedem Quadrat ist die Ordnungszahl eines Buchstabens im Alphabet. Lass uns das Prüfen:

6 + 4 + 4 = 14. "M" ist der vierzehnte Buchstabe im Alphabet. Wir zählen auch "Yo"!
4 + 1 + 7 = 12. "K" ist der zwölfte Buchstabe im Alphabet.
5 + 6 + 10 = 21. "U" ist der einundzwanzigste Buchstabe im Alphabet.
1 + 14 + 2 = 17. "P" ist der siebzehnte Buchstabe im Alphabet, der anstelle des Fragezeichens stehen sollte.

Anstelle eines Fragezeichens sollte die Zahl 179 sein. Wenn Sie sich ab 3 im Uhrzeigersinn bewegen, entspricht jede nachfolgende Zahl dem Doppelten der vorherigen, zu der 1, 3, 5, 7, 9 hinzugefügt wurden.

3 × 2 + 1 = 7.
7 × 2 + 3 = 17.
17 × 2 + 5 = 39.
39 × 2 + 7 = 85.
85 × 2 + 9 = 179.

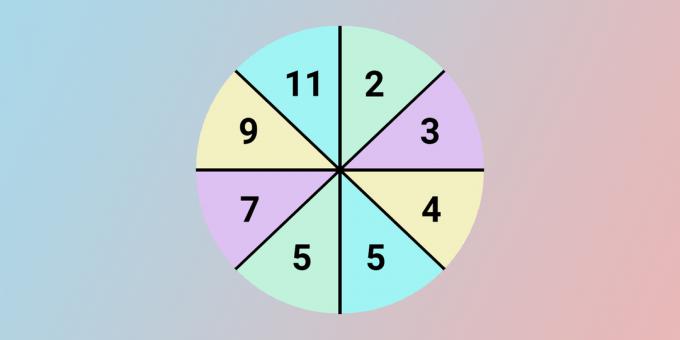
Anstelle eines Fragezeichens sollte die Zahl 11 sein. Um jede Zahl aus der linken Kreishälfte zu erhalten, nehmen wir eine Zahl aus dem gegenüberliegenden Sektor, verdoppeln und addieren eine.

5 = 2 × 2 + 1.
7 = 3 × 2 + 1.
9 = 4 × 2 + 1.
11 = 5 × 2 + 1.

Anstelle eines Fragezeichens sollte die Zahl 66 sein. Wenn wir uns ab 4 im Uhrzeigersinn bewegen, entspricht jede nachfolgende Zahl dem doppelten der vorherigen, von der zwei abgezogen wurden.

4 × 2 − 2 = 8 − 2 = 6.
6 × 2 − 2 = 12 − 2 = 10.
10 × 2 − 2 = 20 − 2 = 18.
18 × 2 − 2 = 36 − 2 = 34.
34 × 2 − 2 = 68 − 2 = 66.